이번 포스팅에서는 Sungyong Baik이 ICCV 2021에서 발표한 "Meta-Learning with Task-Adaptive Loss Function for Few-Shot Learning"을 읽고 정리해 보도록 하겠습니다.
1. Introduction
최근에 meta-learning 방법은 few-shot learning의 한 방법으로 대두되고 있습니다. Meta-learning 중 optimization-based meta-learning은 종종 bi-optimization으로 표현됩니다. Bi-optimization은 일반화 성능을 향상시키기 위한 outer-loop optimization과 적은 데이터를 갖고 있는 태스크에서의 학습을 위한 inner-loop optimization으로 이뤄져 있습니다.
그 중 Model-Agnostic Meta-Learning(MAML)은 일반화 성능을 향상시키기 위해 네트워크 weight의 초기값을 학습시킵니다. 이렇게 학습된 초기값은 적은 데이터에도 모델이 잘 적응할 수 있게 해 줍니다. 그러나, 태스크가 다양하거나 학습 데이터와 테스트 데이터가 상이한 경우에는 MAML의 일반화 성능이 다소 떨어지기도 합니다. 다른 논문에서는 이를 해결하기 위해 더 나은 초기값을 찾거나, 더 빠른 적응을 위한 방법을 적용했으나 이러한 방법들 또한 cross entropy와 같은 간단한 loss function을 적용하는 데 그쳤습니다.
본 논문에서는 inner-loop optimization에 더 나은 loss function을 적용하는데 초점을 두었습니다. 그 결과 본 논문에서는 아래 그림과 같은 Meta-Learning with Task Adaptive Loss Function(MeTAL)을 제안합니다. MeTAL은 adaptive loss function을 학습하여 각각의 태스크에 대해 더 나은 일반화 성능을 보여줍니다. MeTAL은 또한 두 개의 meta-learner를 통해 loss function을 학습시키는데, 하나는 loss function에 대한 meta-learner이고, 다른 하나는 learned loss function으로부터 parameter를 생성하는 meta-learner입니다. MeTAL은 labeled data와 unlabeled data 모두에 적용 가능합니다.

2. Related Work
Few-shot learning에서의 meta-learning은 이전의 태스크로부터 얻은 선험 지식을 이용해 새로운 태스크에 오버피팅 없이 적응하는 것이 목적입니다. 선험 지식을 어떻게 학습하고, task adaptation을 어떻게 하는지에 따라 여러 meta-learning 방법들이 존재합니다.
Metric-based 방법은 선험 지식을 임베딩 공간에 표현하여 비슷한 클래스들이 가까이에 위치하도록 합니다. Black-box 또는 network-based 방법은 별도의 네트워크나 메모리를 사용하여 weight를 생성하거나 갱신하거나 예측합니다. 이에 반해 optimization-based 방법은 bi-level optimization을 적용하여 초기화나 weight 갱신과 같은 학습 과정을 학습하여 새로운 태스크에서 사용합니다.
본 논문에서는 유명한 optimization-based 방법인 MAML에 집중했습니다. 앞서 언급했듯이 몇몇의 개선된 MAML 방법들 또한 간단한 loss function을 사용합니다. 그러나 현대의 딥러닝 프레임워크에서는 대부분 L2 regularization과 같은 auxiliary loss term을 사용합니다. 최근의 개선된 MAML 방법들 또한 auxiliary loss term을 사용했지만, 대부분 fixed loss function을 사용했습니다. 그렇기 때문에 태스크 별로 loss function이 다르게 필요한 경우에도 불구하고 같은 loss function을 사용합니다. 따라서 본 논문에서는 meta-network에서 학습된 MeTAL을 도입하여 높은 성과뿐만 아니라 간단하고 다른 meta-learning 알고리즘에도 적용 가능하게 했습니다.
3. Proposed Method
3.1. Preliminaries
Meta-learning 프레임워크에서는 태스크들의 모음
보통 support set의 크기에 따라 k-shot task라고 불리기도 합니다. 태스크 별로 학습된 base learner는
MAML은 선험 지식을 learnable initialization에 사용하여 base learner의 weight가 좋은 초기값으로 작용하게 합니다. 이 과정에서 bi-level optimization을 수행하는데, inner-loop optimization에서는 base learner가 learnable initialization
Outer-loop optimization에서는
3.2. Meta-learning with Task-Adaptive Loss Function (MeTAL)
본 논문에서는 loss function 자체를 meta-learn하여 전체 adaptation 과정이나 inner-loop optimization을 규제하도록 합니다. Inner-loop optimization loss function인
여기서
여기서
여러 태스크에 걸쳐 일반화 성능을 향상시키기 위해 outer-loop optimization은 다음과 같이 진행됩니다.
본 알고리즘을 pseudo code로 표현하면 다음과 같습니다.

MeTAL에서 meta-learner로 사용된

본 논문에서는
4. Experiments
본 논문에서는 MeTAL의 성능을 시험하기 위해 few-shot classification, cross-domain classification, few-shot regression에 대해 실험을 진행했습니다. 여기서 MeTAL은 semi-supervised로 실행되었습니다.
4.1. Few-shot classification
사용된 데이터셋은 miniImageNet과 tieredImageNet입니다. 본 논문에서는 MeTAL과 다른 MAML 기반의 방법들을 5-way, 5-shot과 5-way 1-shot 환경에서 실험을 진행했습니다. 실험 결과는 아래와 같습니다.
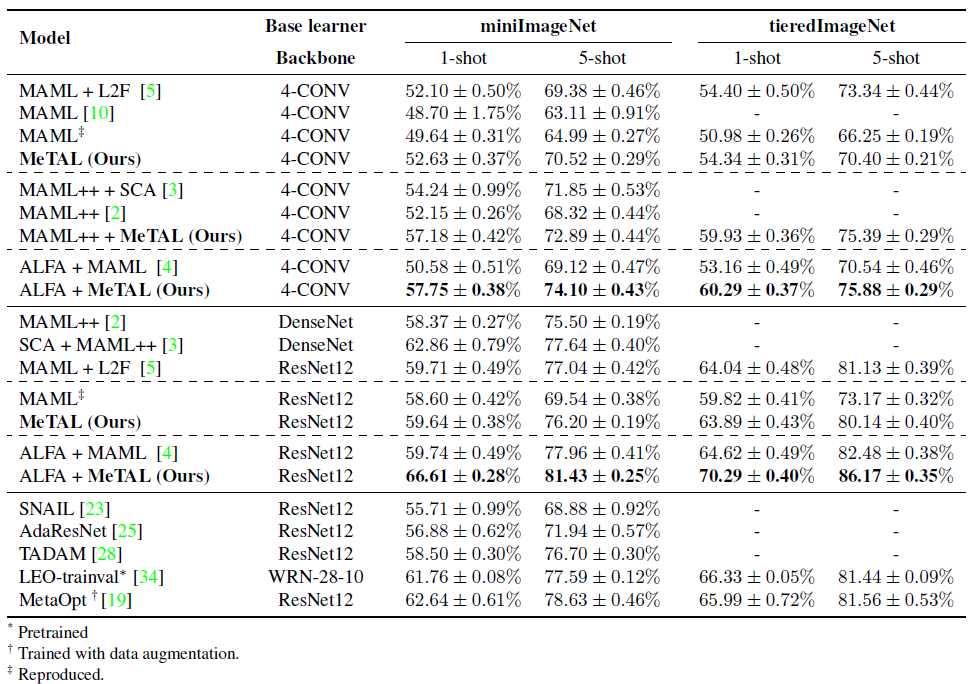
실험 결과 MeTAL의 성능이 우수할 뿐만 아니라 다른 MAML++나 ALFA와 같은 MAML 기반의 알고리즘에도 MeTAL을 성공적으로 적용할 수 있음을 알 수 있습니다. 또한, ALFA + MeTAL의 경우 상대적으로 큰 네트워크인 DenseNet, ResNet, WideResNet을 적용한 다른 알고리즘보다도 효과적으로 성능이 개선됐음을 알 수 있습니다.
4.2. Cross-domain few-shot classification
Cross-domain few-shot classification은 학습 데이터와 테스트 데이터의 차이가 매우 컸을 때를 가정하고 진행한 실험입니다. Meta-learning의 경우 선험 지식에 과도하게 의존하면 새로운 도메인에 대해 쉽게 meta-overfitted됩니다. Meta-overfitting이 발생하게 되면 새로운 태스크에 대해 adapt하기 힘들어집니다.
사용된 데이터셋은 miniImageNet을 학습 데이터로, CUB를 테스트 데이터로 사용했습니다. 결과는 다음과 같습니다.
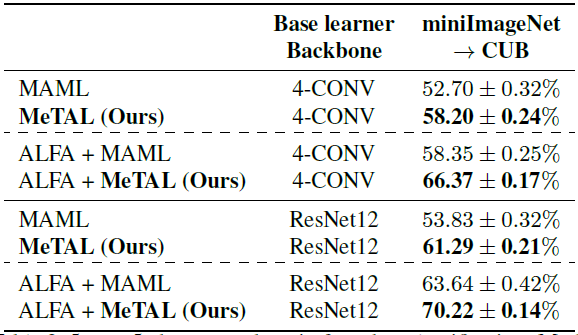
MeTAL은 cross-domain 환경에서도 성능이 우수한 것을 볼 수 있습니다. 다른 방법과의 격차가 few-shot classification보다 커졌는데, 이는 MeTAL이 task-adaptive loss function으로 인해 domain gap에 대해 robust하단것을 보여줍니다.
4.3. Few-shot regression
그리고 MeTAL의 flexibility와 applicability를 보여주기 위해 few-shot regression에 대해서도 실험을 진행했습니다. Target function

4.4. Ablation studies
본 논문에서는 task state, learning of a loss function, task-adaptive loss function, semi-supervised inner-loop optimization에 대한 효과를 알아보기 위해 ablation study를 진행했습니다. Albation study에서는 4-conv backbone과 5-way 5-shot classification을 진행했습니다.
첫 번째는 learning inner-loop optimization loss function(

learned loss는 효과가 있었고, (2)와 (3)이 큰 차이가 나지 않는 것을 보아 learned loss가 입력으로 주어진 cross entropy loss 정보를 유지한다고 볼 수 있습니다.
두 번째는 task-adaptive loss function(
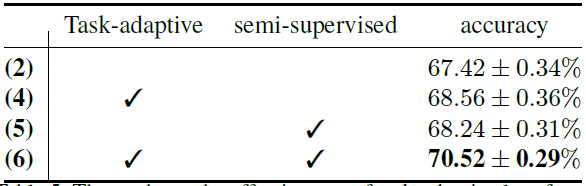
(2)에 비해 (4)가 성능이 우수하여 task-adaptive function은 효과가 있었고, (2)보다 (5)가 우수하여 query set을 사용한 것 또한 효과가 있었습니다. 그러나 (4)와 (5) 모두 본 논문의 방법인 MeTAL((6)) 보다는 성능이 떨어졌습니다.
이번에는 task state의 각 요소에 따른 효과를 실험했습니다.

4.5 Visualization
이번에는 meta learner g에서 생성된 affine transformation parameter
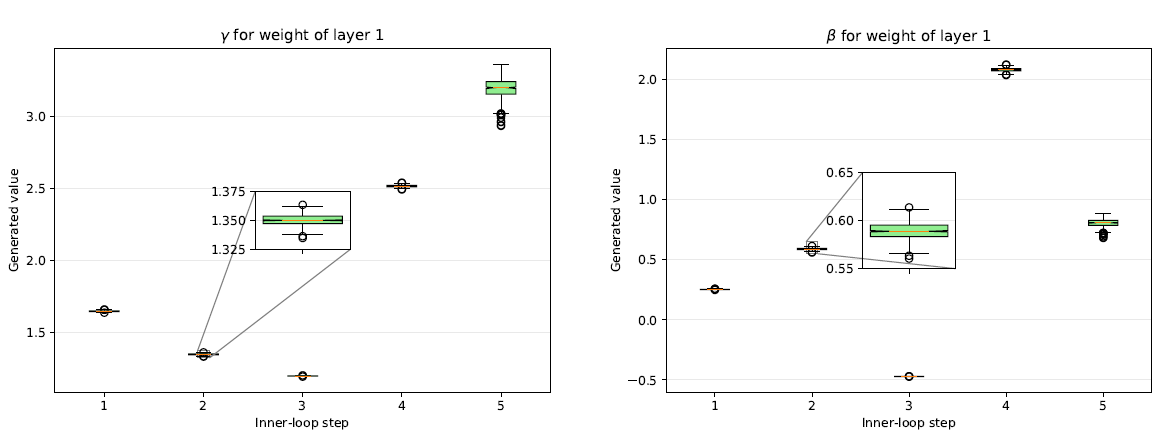
5. Conclusion
본 논문에서는 few-shot learning을 위한 task-adaptive loss function을 제안했습니다. MeTAL은 inner-loop optimization동안 current task state를 바탕으로 loss function을 각각의 task에 적응시킵니다. 그 결과 각각의 태스크에서 더 나은 일반화 성능을 기대할 수 있게 됩니다. MeTAL은 여러 MAML 기반 알고리즘에 적용 가능했습니다. 또한, semi-supervised inner loop optimization도 가능케 했습니다.
Reference
[1] https://arxiv.org/abs/2110.03909




댓글