이번 포스팅에서는 Shuo Yang이 ICLR 2021에서 발표한 "Free Lunch for Few-shot Learning: Distribution Calibration"을 읽고 정리해 보도록 하겠습니다.
1. Introduction
데이터를 수집하고 labeling 하는 데 상당한 비용이 들기 때문에 적은 수의 데이터(few-shot)로 학습을 진행하는 것은 많은 주목을 받고 있습니다.

위 그림에서 별표는 주어진 데이터이고, 색칠된 영역은 해당 class가 실제로 차지하는 영역입니다. 일반적인 few-shot 환경에서는 모델이 별 표시를 기준으로 검은 실선처럼 class들을 구분 짓지만, 각 데이터는 실제 영역의 극히 일부에 지나지 않습니다. 이러한 문제를 해결하기 위해 많은 시도가 있었습니다. Finn et al.과 Snell et al.은 meta-learning 방법으로 few-shot task에서 adaptation을 하도록 했고, Hariharan & Girshick은 생성 모델을 통해서 데이터나 feature들을 합성시켜 데이터의 양을 늘렸습니다. Ren et al.은 unlabeled data와 pseudo label을 이용했습니다.
이전의 방법들은 대부분 강력한 모델을 개발하는 것에 초점을 두었습니다. 그러나 본 논문에서는 위 그림에서 나타난 biased-distribution을 calibrate하여 calibrated distribution의 데이터를 학습에 이용하였습니다. 본 논문에서는 모든 feature vector의 차원들은 Gaussian distribution을 따르고 비슷한 class에 대해서는 비슷한 distribution을 따른다는 가정을 세웠습니다.

위 표는 북극 여우와 다른 동물들 간의 distribution이 얼마나 유사한지 나타낸 표입니다.



비슷한 class들 간의 similarity가 높게 나오는 것을 알 수 있습니다.
이러한 distribution을 파악하기 위해서는 충분한 데이터가 필요합니다. 그래서 본 논문에서는 충분한 데이터를 가진 class로부터 distibution을 구하고, 이런 distribution 중 에서 similarity를 기준으로 few-shot classes에 transfer시켰습니다.
2. Related Works
Few-shot classification은 meta-learning을 통해 few-shot task에서 빠르게 adapt 하도록 연구되었습니다. 이러한 meta-learning 알고리즘 중 optimization-based 알고리즘은 gradient descent procedure를 initialization, update direction, learning rate 등에서 최적화시키는 방법입니다. MatchingNet과 ProtoNet은 metric-learning 기반의 meta-learning 방법을 취했습니다. 이 방법들은 각각의 class를 대표하는 지점과의 거리를 계산하며 분류했습니다. 본 논문의 방법은 새로운 parameter를 도입하지 않고 일반적인 supervised learning 방법으로 학습합니다.
데이터를 생성하는 것도 few-shot setting에서 적용할 수 있습니다. 대부분의 방법은 GAN이나 autoencoder를 통해 sample이나 feature를 생성하여 training set을 augment합니다. 그 방법에는 adversarial generator conditioned on tasks를 도입하여 합성된 데이터를 생성하는 방법, variational autoencoder를 학습시켜 distribution과 predicted label를 추정하는 방법이 있습니다. Autoencoder의 경우 visual space와 sematic space를 추정하여 샘플링하거나 intra-class deformation을 인코딩하는 데 사용됐습니다. 그리고 또, class hierarchy를 통해 feature를 생성하는 방법도 있습니다. 이러한 방법들은 복잡한 모델과 loss function을 설계해야 합니다. 그러나 본 논문의 방법은 매우 간단합니다.
Data augmetation으로는 unsupervised few-shot learning에서 pretext task를 구성하기 위한 방법을 쓰거나, hallucinaiton model을 설계해 모델에 입력에 따른 다른 augmented 버전을 생성하는 방법도 있습니다. 아니면, 여러 feture들을 concatenate하거나 intra-class variance를 이용하여 feature representation을 augment하는 방법도 있습니다. 이러한 방법들은 원본 sample이나 feature distribution으로부터 augment를 학습하는 것인데, 본 논문에서 예측하고자 하는 것은 class level distribution이고 그래서 하나의 sample에 대해 inductive bias를 없앨 수 있으며 calibrated distribution으로부터 다양한 sample을 획득할 수 있습니다.
3. Main Approach
3.1 Problem Definition
본 논문에서는 전형적인 few-shot classification setting을 따릅니다. 우선 다음과 같은 dataset D가 주어집니다.
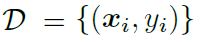
여기서 x_i는 y_i의 feature vector입니다. y_i는 class 집합 C의 원소입니다. 이제 class 집합 C는 base class C_b와 novel class C_n으로 나뉠 수 있습니다. 집합 C_b와 C_n의 관계는 다음과 같습니다.

학습 목표는 base class의 데이터로 모델을 학습 시켜 몇몇 novel class의 원소로 이루어진 task에서 잘 generalize하는 것입니다. 이때 각 task에는 적은 labeled data만 제공됩니다(few-shot task). 보통 이런 task를 N-way-K-shot task라고 불리는데 여기서 N은 class의 개수이고, K는 각 class마다 제공되는 데이터의 수입니다. 그래서 novel class에서는 데이터를 이제 support set과 query set으로 나뉘게 됩니다. Support set은 novel class의 원소로 이루어진 task에서 학습 데이터에 해당합니다. 총 NxK개의 원소로 이루어져 있습니다. 그리고 query set은 테스트 데이터에 해당하며 q개의 test case로 구성되어있습니다. 두 set의 표현은 아래와 같습니다.
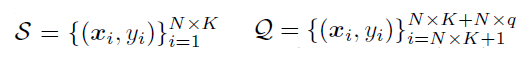
최종적으로 모델의 성능은 novel class의 원소들로 이루어진 여러 task들에서 query set에 대한 평균 accuracy로 평가됩니다.
3.2 Distribution Calibration
앞서 언급된 것 처럼 base class는 충분한 데이터를 갖고 있습니다. 이러한 base class로 부터 계산된 distribution은 novel class에서 샘플링된 task에서 측정된 distribution보다 더 정확합니다. 아까 1장의 북극여우의 예시와 같이 비슷한 유형의 class들은 distribution도 비슷한 것을 알 수 있습니다. 그래서 이러한 statistic들이 base class에서 novel class로 얼마나 비슷한 지 알 수 있다면 transfer할 수 있습니다.
본 논문에서는 Mangla et al.의 연구에서 사용된 pretrained WideResNet을 사용했습니다.
3.2.1 Statistics of The Base Classes
i번째 base class의 feature vector의 mean은 다음과 같이 구할 수 있습니다.
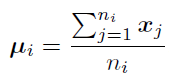
이때, x_j는 base class의 j번째 feature vector이고 n_i는 class i의 sample의 개수입니다. 그리고 class i의 covariance matrix는 다음과 같습니다.
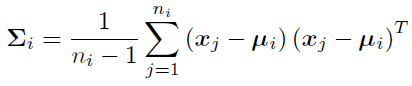
3.2.2 Calibrating Statistics of The Novel Classes
이번에는 novel class에서 샘플링된 N-way-K-shot task에서 다뤄보겠습니다. 본 논문에서는 distribution의 skewness를 줄이고 distribution을 좀 더 Gaussian에 가깝게 하기 위해 Tukey's Ladder of Powers transformation을 적용했습니다. Tukey's Ladder of Powers transformation은 다음과 같습니다.
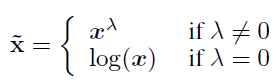
여기서 λ는 hyper-parameter입니다. λ=1이면 원래 x와 같고, λ를 작게 조절하면 postitive-skewness가 감소하게 됩니다.
그다음에는 Euclidean distance를 이용하여 base class feature의 mean(Equation 1)과 novel class의 거리를 구합니다. 이후 과정을 위해 가장 가까운 base class와의 거리가 가장 크도록 하기 위해 -1을 곱해줍니다.
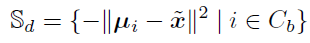
그렇게 되면 S_d에는 한 novel class와 여러 base class간의 거리에 음을 곱한 값이 저장되어있습니다. 이를 가장 큰(가장 가까운) k개의 base class의 인덱스를 뽑습니다. 식은 다음과 같습니다.
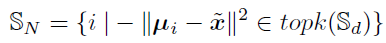
만약 k가 2라면 해당 novel class로 부터 가장 가까운 두 base class의 index가 S_N에 들어가게 됩니다. 이번엔 이 k개 base class의 statistic을 사용하여 disribution calibration을 진행합니다.
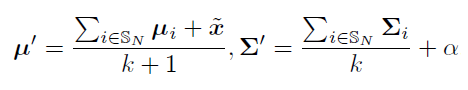
여기서 α 또한 hyper-parameter으로 calibrated distribution으로부터 추출되는 sample의 dispersion을 조절합니다. 이러한 과정을 N-way-K-shot에서 K개의 sample에 대해 진행합니다. 그렇게 되면 novel class y에 대해 다음 set of statistics가 얻어집니다.
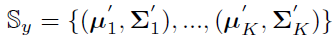
3.2.3 How to Leverage The Calibrated Distribution?
이번엔 이러한 calibrated distribution을 어떻게 학습에 활용하는지 설명해 보겠습니다. 위 S_y로부터 feature vector를 sample할 수 있습니다.
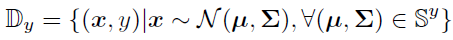
이렇게 sampling된 데이터와 기존의 original support set feature S를 둘 다 사용하여 loss function으로 cross-entropy를 사용하여 학습시킵니다.
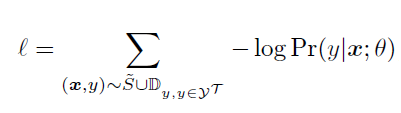
이때, S에도 tilde(~)가 붙어있는데, equation 3에서 처럼 Tukey's Ladder of Powers transformation을 적용했기 때문입니다.
4. Experiments
4.1 Experimental Setup
4.1.1 Datasets
사용된 데이터셋은 miniImageNet, tieredImageNet, CUB입니다. miniImageNet은 ILSVRC-12 데이터셋에서 파생되었습니다. 100가지의 class를 갖고 있고 각 class마다 600장의 이미지가 있습니다. 이미지의 크기는 84x84x3이며, 64 base class, 16 validation class, 20 novel class로 나누었습니다.
tieredImageNet 또한 ILSVRC-12에서 파생된 좀 더 큰 데이터셋입니다. 608가지의 class로 이루어져 있고, 이는 34개의 상위 class로 묶입니다. 각 class마다 평균 이미지의 수는 1281장이며, 351 base class, 97 validation class, 160 novel class로 나누었습니다.
CUB는 fine-grained few-shot classification benckmark입니다. 200가지의 bird class로 이루어져 있고 전체 이미지의 수는 11788장입니다. 이미지의 크기는 84x84x3이며, 100 base class, 50 validation class, 50 novel class로 나누었습니다.
4.1.2 Evaluation Metric
위 세가지 데이터셋으로 10000 이상의 task에서 5-way-1-shot과 5-way-5-shot에서 top-1 accuracy의 평균을 측정했습니다.
4.1.3 Implementation Details
Feature extractor로 WideResNet을 사용했는데, Mangla et al.의 학습 방식을 따랐습니다. 각각의 데이터셋마다 base class로 학습하고 novel class로 테스트를 진행했습니다. 이때, feature은 feature extractor의 뒤에서 두 번째 layer의 output에 ReLU를 적용시킨 feature vector를 사용했습니다. ReLU를 적용하여 feature vector가 0 이상이기 때문에 equation 3을 적용시킬 수 있었습니다. Distribution calibration stage에서는 앞서 언급한 바와 같이 base class의 statistics를 구하여 각 데이터셋마다 novel class distribution을 calibrate하기 위해 transfer했습니다. 본 논문에서는 scikit-learn의 LR(Logisitic Regression)과 SVM을 사용했습니다. 모든 데이터셋에서 equation 6의 α를 제외하곤 같은 hyperparameter를 사용했는데, miniImageNet과 tieredImageNet에서는 α=0.21, CUB에서는 α=0.3을 사용했습니다. 그리고 (number of generated feature)=750, λ=0.5, k=2를 사용했습니다.
4.2 Comparison to State-of-The-Art
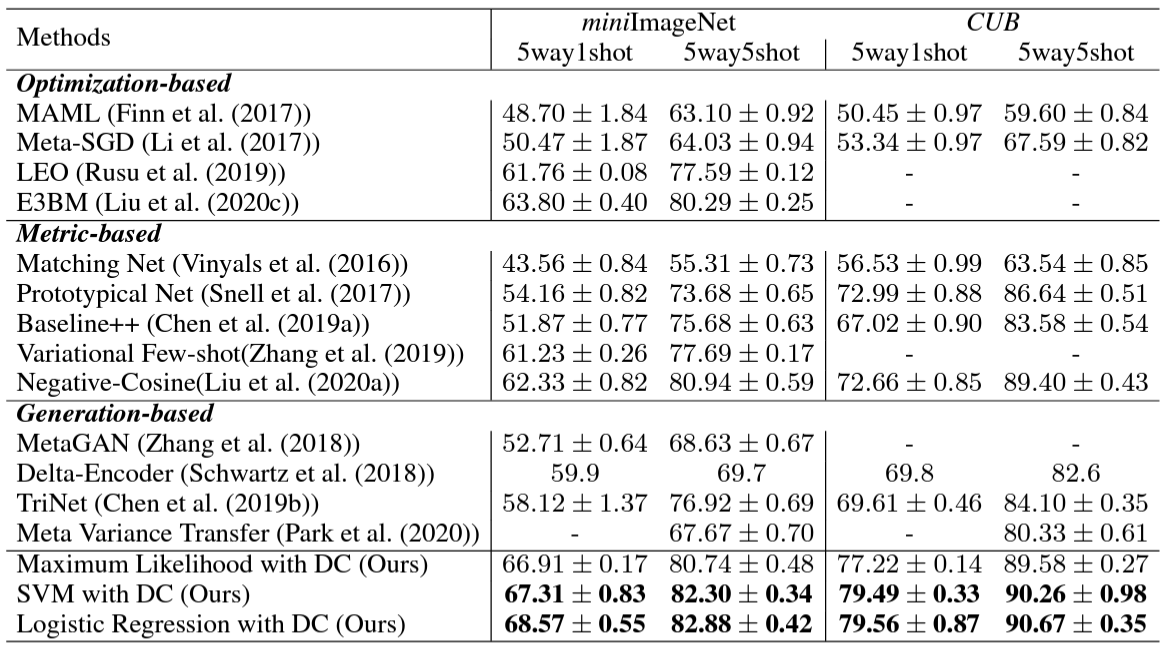
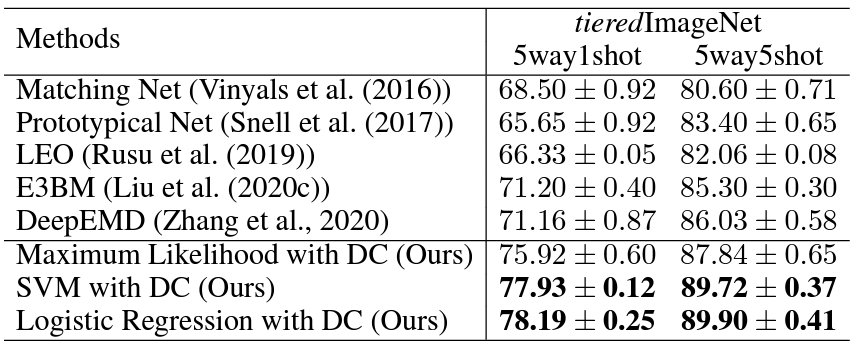
위 두 표는 세가지 데이터셋에 대해 본 논문의 방법을 다른 SoTA와 비교한 것입니다. 본 논문의 방법은 다른 classifier에 대해서도 적용 가능합니다. 그를 보여주기 위해 간단한 classifier인 SVM와 Logistic Regression에 적용했습니다. 간단한 classifier를 적용했음에도 불구하고 본 논문의 방법이 다른 sota 모델들보다 월등히 우수했습니다. 심지어 5way1shot setting에서는 generation-based 방법보다 약 10%p 좋은 성능이 나왔습니다. Generative-model의 경우 모델을 설계하고 학습해야 하기 때문에 시간과 비용이 많이 소모되지만 본 논문의 방법은 간단하고, 효과적이고 유연합니다. 본 논문의 방법 중 Maximum Likelihood는 다른 모든 sota 방법보다 우수했고, SVM과 LR은 더 우수한 성능을 보였습니다.
4.3 Visualization of Generated Samples
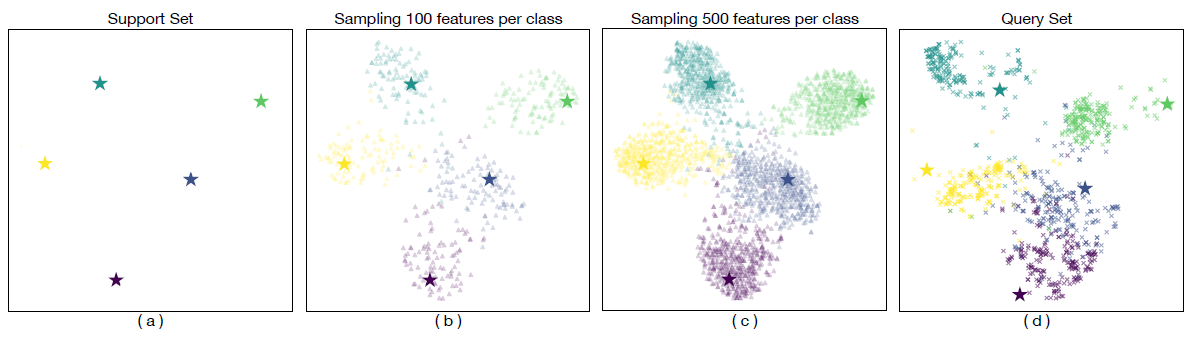
위 사진은 support set, sampling 100, sampling 500, query set에 대해 t-SNE visualization을 실험한 결과입니다. 우선 support set이 query set의 분포와 많이 어긋나있고, distrubution calibration을 진행한 결과, sampled feature가 query set의 distribution에 어느 정도 겹치는 모습을 확인할 수 있습니다.
4.4 Applicability of Distibution Calibration
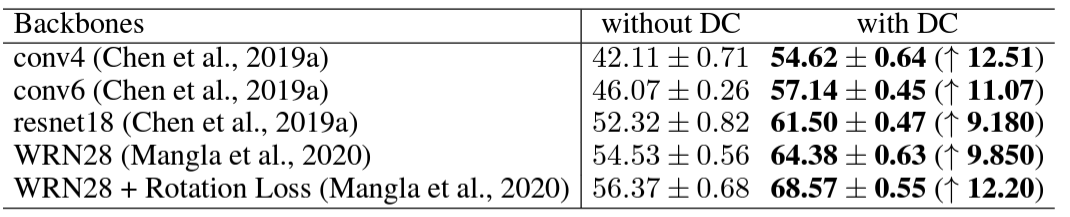
위 표는 Distribution Calibration을 여러 backbone network에 적용시킨 모습입니다. DC를 적용시키면서 대략적으로 10%p정도의 성능 향상이 있었습니다.

이번에는 다른 few-shot classification 알고리즘에 DC를 적용시켜 본 결과입니다. 대략적으로 12%p정도의 성능 향상이 있었습니다.
4.5 Effects of Feature Transformation and Training with Generated Features
본 논문에서는 Tukey's Ladder of Powers transformation과 generated feature의 유무에 따른 ablation study도 진행했습니다.

둘 다 사용하지 않았을 때는 10% 정도의 심각한 성능 저하가 있었고, 둘중 하나라도 사용하지 않았을 땐 5%의 성능 저하가 있었습니다.
그리고 본 논문에서는 최적의 λ값과 샘플의 수에 따른 성능의 변화를 찾기 위한 실험도 진행했습니다.
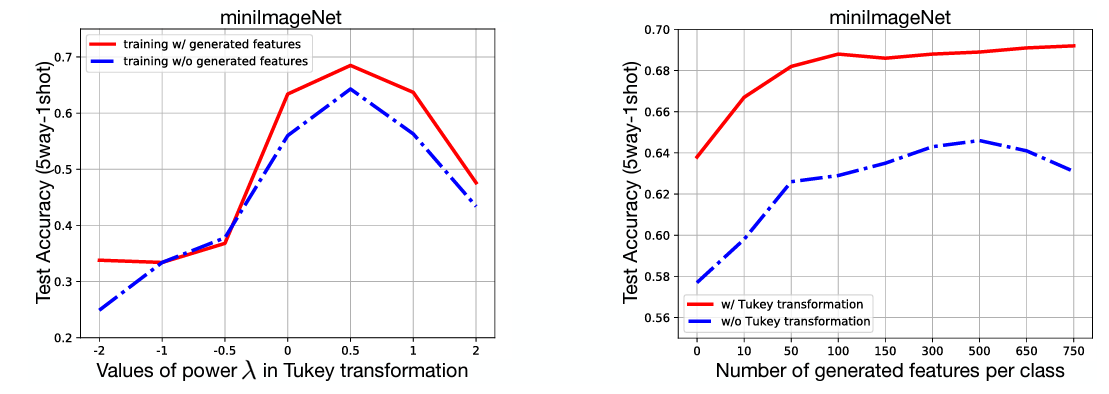
실험 결과 λ=0.5가 최적값으로 도출되었고, 샘플의 수가 500 이전에는 샘플의 수가 증가함에 따라 성능도 같이 증가했지만, 500 이후로는 transformation을 하지 않으면 오히려 성능이 하락했습니다.
4.6 Other Hyper-parameters
마지막으로 한 novel class에서 가장 가까운 base class의 개수인 k와 equation 6에서 생성된 샘플의 dispersion을 조절하는 α값에 따른 성능의 변화도 실험했습니다.
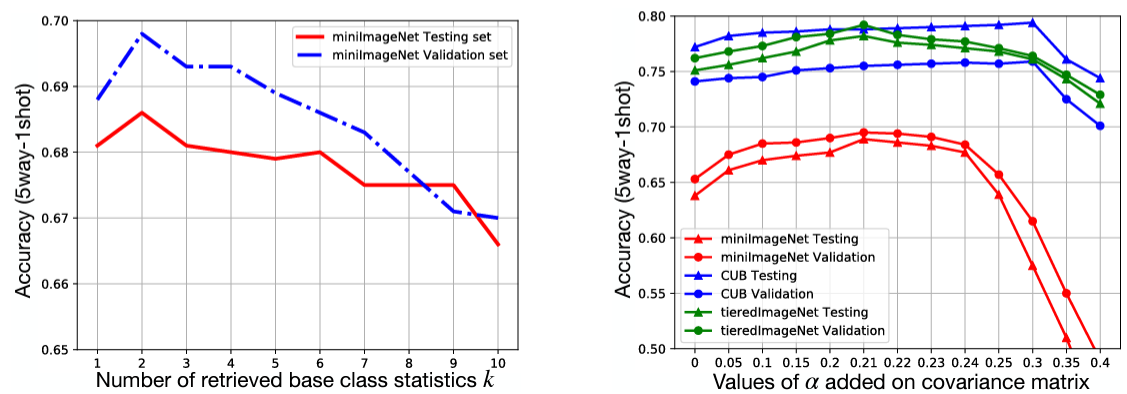
k=2일 때 가장 좋은 성능이 나왔고, α는 데이터셋마다 다른 값에서 가장 좋은 성능을 보였습니다.
5. Conclusion and Future Works
본 논문에서는 few-shot classification을 위한 간단하고 효과적인 distribution calibration strategy를 제안했습니다. 복잡한 generative model, loss function 다른 추가의 parameter없이도 본 논문의 방법을 적용한 간단한 logistic regression만을 적용해도 miniImageNet기준 다른 sota 모델들보다 성능이 우수하게 나왔습니다. Calibrated distribution은 visualized되어 feature distribution을 정확하게 따라가고 있다는 것을 알 수 있었습니다. Future work에서는 multi-domain few-shot classification이나 metric-based meta-learning 알고리즘 등 다양한 문제 환경에서 distribution calibration의 적용 가능성을 탐구해 보겠다고 합니다.
References
[1] https://arxiv.org/abs/2101.06395v3
[2] https://ko.m.wikipedia.org/wiki/%ED%8C%8C%EC%9D%BC:Howling_White_Wolf.jpg
[3] https://en.wikipedia.org/wiki/Arctic_fox
[4] https://en.wikipedia.org/wiki/Beer_bottle




댓글