이번 포스팅에서는 Karras et al.이 CVPR 2019에서 발표한 "A Style-Based Architecture for Generative Adversarial Networks" 를 읽고 정리해보도록 하겠습니다.
해당 논문은 StyleGAN으로 잘 알려져 있으며 이후 발표된 StyleGAN2, 3 모두 SOTA를 달성하고 있고
현재 GAN을 대표하고 있습니다. StyleGAN은 PGGAN을 베이스로 연구되었습니다.
1. Introduction
GAN을 이용하여 생성하는 이미지의 품질과 해상도는 급격하게 증가하고 있습니다. 그러나, 이러한 GAN들은 실제로 어떻게 작동되는지 알 수 없는 blackbox와 같고, latent space에 대한 속성들은 잘 설명되지 않습니다. Style transfer 분야에 영감을 받아, 본 논문에서는 이미지 생성 과정을 노출시켜 이를 컨트롤하도록 하는 generator를 고안했습니다. StyleGAN의 generator는 learned constant input 부터 시작하여 각 conv layer에서 style을 변경하는 식으로 이미지를 생성합니다. 그 결과, pose 또는 identity와 같은 high-level attribute와 freckles나 hair와 같은 stochastic variation이 분리되어 학습됩니다.
StyleGAN은 latent code z를 intermediate latent code w로 변환합니다. 학습을 진행할 때, 전통적인 GAN들은 latent code z가 training data의 distribution을 따라가도록 학습이 되는데 이 경우에서 불가피하게 entanglement가 발생하게 됩니다. 그러나, latent code z를 intermediate latent code w로 변환하게 되면 w는 보다 disentangle되게 됩니다. 본 논문에서는 이러한 distentanglement를 확인하기 위해 perceptual path length와 linear separability를 이용했습니다.
2. Style-based generator
전통적으로 latent code z는 generator에 input layer를 통하여 입력으로 들어갑니다. StyleGAN의 generator에서는 모델의 input layer를 제거하고 대신에 learned constant input으로 입력을 줍니다. Latent code \(z{\in}\mathcal{Z}\)는 대신에 non-linear mapping network \(f:\mathcal{Z}\rightarrow\mathcal{W}\)를 통해 intermediate latent code \(w{\in}\mathcal{W}\)로 변환됩니다.
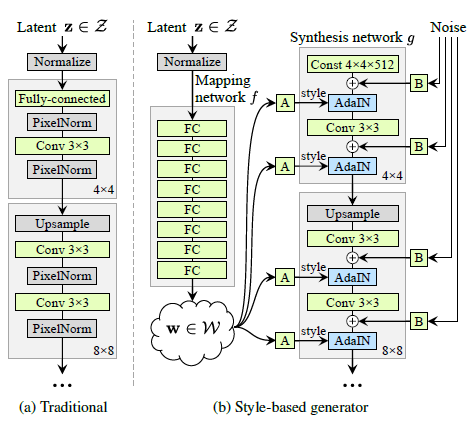
\(z{\in}\mathbb{R}^{512}\)로 부터 생성된 \(w{\in}\mathbb{R}^{512}\)들은 모든 layer에 똑같이 들어가게 됩니다. 위 그림에서 A라고 표시된 부분이 있는데 이는 주어진 \(w\)를 style \(y=(y_s,y_b)\)로 변환시켜주는 learned affine transformation입니다. 그래서 계산된 style은 아래와 같이 AdaIN을 진행하게 됩니다.
\[AdaIN(x_i,y)=y_{s,i}\frac{x_i-\mu(x_i)}{\sigma(x_i)}+y_{b,i}\]
또한, 위 그림에서 B에 해당하는 부분은 noise injection에 해당하는데, stochastic variation을 위한 것입니다. 보다 상세한 내용은 3.2와 3.3절에서 소개하겠습니다.
2.1. Quality of generated images
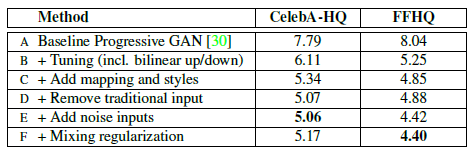
위 표는 CelebA와 FFHQ에 대해 FID를 측정한 결과입니다. (B)는 기존의 PGGAN을 bilinear up/downsampling과 longer training, hyparameter tuning으로 개선시킨 것입니다. 거기에 (C)에서는 mapping network와 AdaIN을 추가한 것입니다. (D)에서는 4x4x512의 constant input으로 모델의 입력을 시작하도록 변경한 것입니다. 마지막으로 (E)에서는 noise input을 이용하여 stochastic variation을 향상시켰고, (F)에서는 mixing regularization을 통해 주어진 latent code를 서로 섞어 더 세밀한 control이 가능해졌습니다.
CelebA에 대한 실험을 할 때는 WGAN-GP만 적용시켰고, FFHQ에서 (A)에는 WGAN-GP만 적용시켰고 (B)~(F)에서는 non-saturating loss와 R1 regularization도 적용시켰습니다.

위 사진은 FFHQ 데이터로 학습시킨 모델이 생성한 이미지들입니다. 위 실험에서는 \(\mathcal{W}\)의 극단적인 부분에서의 샘플링을 막기 위해 truncation trick(\(\psi=0.7\))을 적용시켰습니다. Truncation trick은 우선 여러 \(z\)에 대해 mapping network를 통과시켜 \(w\)들을 얻어내고 \(w\) 들의 평균 \(\bar{w}\)을 얻어냅니다. 그다음, 새로 주어진 \(w\)가 평균 \(\bar{w}\)에서 많이 벗어나지 않도록 아래와 같이 조정해 줍니다.
\[w'=\bar{w}-\psi(w-\bar{w})\]
이러한 truncation에서 \(\psi\)에 따른 이미지 생성 결과는 아래와 같이 나타납니다.

3. Properties of the style-based generator
3.1. Style mixing
StyleGAN에서는 mixing regularization을 적용합니다. Latent code \(z_1,z_2\)가 있을 때, 이를 mapping network에 통과시키면 intermediate latent code \(w_1, w_2\)가 만들어지게 됩니다. 이를 랜덤으로 선택된 point를 두어 이전에는 \(w_1\)를 사용하고 이후에는 \(w_2\)를 사용하는 것입니다. 간단한 소스코드로 예시를 들자면, 아래와 같습니다.
w1 = mapping_net(z1) # [b, 512]
w2 = mapping_net(z2) # [b, 512]
w1 = w1.unsqueeze(1).repeat(1, 18, 1) # [b, 18, 512]
w2 = w2.unsqueeze(1).repeat(1, 18, 1) # [b, 18, 512]
i = np.random.randint(0, 18)
w = torch.cat([w1[:, :i, :], w2[:, i:, :]], dim=1)아래 표는 mixing regurization을 trainng image에서 얼마나 적용시켰는지에 따른 성능을 비교한 것입니다.

3.2. Stochastic variation
사람의 얼굴에서 hair, stubble, freckle 또는 skin pore의 정확한 위치는 일종의 stochastic variation으로 볼 수 있습니다. 이러한 것들은 이미지의 identity를 크게 바꾸지 않는 선에서 변경될 수 있습니다. 이를 StyleGAN에서는 convolution layer의 output에 randomized noise를 픽셀 별로 더하는 것으로 진행합니다.

위 이미지에서 noise가 identity는 내버려 둔 채 머리카락의 위치와 같은 stochastic variation만 컨트롤하는 것을 볼 수 있습니다.

위 이미지는 noise를 어느 레이어에 주었는지에 따른 실험 결과입니다. (a)는 노이즈를 모든 레이어에, (b)는 노이즈를 사용하지 않고, (c)는 (64x64-1024x1024)의 fine layer에만, (d)는 (4x4-32x32)의 coarse layer에만 적용시킨 것입니다.
3.3. Separation of global effects from stochasticity
StyleGAN의 style은 pose, lighting, background style과 같은 global effect를 가지고 있습니다. 왜냐하면 온전한 feature map이 style을 통해 scaled와 biased 되기 때문입니다. 반면에, noise는 각 픽셀에 독립적으로 더해지기 때문에 stochastic variation에 좀 더 적합합니다.
4. Disentanglement studies
본 논문에서는 disentanglement를 latent space가 linear subspace로 구성되어 있어 하나의 subspace가 하나의 variation만 담당하는 것이라고 정의합니다.
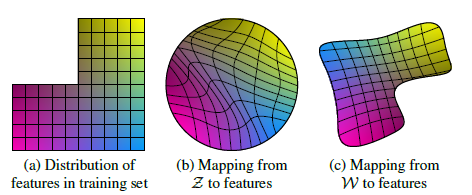
위 그림의 예시에서, (a)는 가로 또는 세로를 따라 점을 이동시키면 다른 것은 변화하지 않습니다. 그러나 (b)에서는 가로 또는 세로로 점을 이동시키면 다른 것도 같이 변화하게 됩니다. 그래서 (b)는 entangle 되어있다고 합니다. 이에 반해, mapping network는 (c)에서처럼 z를 w로 변환시켜 보다 disentangle되게 latent space를 만들었다고 볼 수 있습니다.
4.1. Perceptual path length
본 논문에서는 latent space의 disentanglement를 측정하기 위해 perceptual path length를 사용합니다. 선 요약하자면, 두 latent \(z_1, z_2\) 또는 \(w_1, w_2\) 사이에서 \(t\) 위치와 \(t+\epsilon\) 위치에서 interpolate 시킨 두 latent가 얼마나 perceptually distant한가 측정한 것입니다. z에 대해서는 spherical interpolation, w에 대해서는 linear interpolation을 사용합니다.
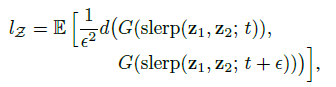
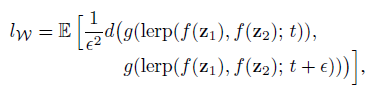
여기서 f는 mapping network, d()는 LPIPS입니다. 실험 결과는 아래와 같습니다.
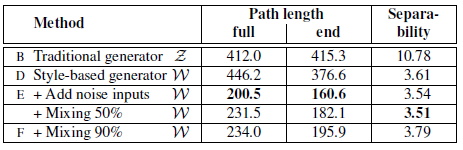
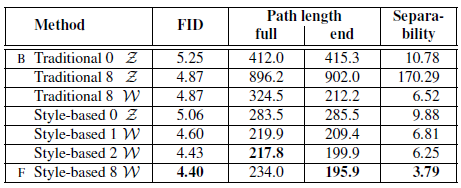
위 표는 mapping network가 path length에 얼마나 영향을 주는지 나타낸 것입니다.
4.2. Linear separability
Latent space가 충분히 disentangle되어있다면, 이미지의 variation에 따른 latent의 variation direction을 찾을 수 있습니다. 본 논문에서는 latent space의 point가 linear hyperplane을 통해 얼마나 잘 분리되는가를 측정합니다. 본 논문에서는 discriminator와 유사한 binary classification network를 사용하여 male과 female과 같은 binary attributes들을 분류하도록 학습시킵니다. 이러한 attribute들은 CelebA의 40가지 attribute를 활용했습니다. 하나의 attribute의 separability를 측정하기 위해 200,000개의 이미지를 샘플링하고 분류합니다. 그다음에 classifer confidence가 높은 반만 취합니다.
각각의 attribute에 대해 SVM을 학습시켜 주어진 latent(z 또는 w)가 binary attribute에서 어느 편에 위치하는지 분류합니다. 그다음에 conditional entropy \(H(Y{\vert}X)\)를 측정하는데, X는 SVM으로, Y는 classifer로 측정된 class입니다. 이를 통해 얼마나 많은 additional information이 실제 sample의 class를 맞추기 위해 필요한지 표현이 되고, 낮은 값은 variation에 따른 latent의 변화가 consistent하고 따라서 disentangle이 잘 되어있다고 볼 수 있습니다. 최종적으로는 40개의 attribute \(i\)에 대해서 \(exp(\sum_i{H(Y_i{\vert}X_i)})\)로 측정합니다.
References
[1] https://arxiv.org/abs/1812.04948



댓글