[Algorithm] Bellman-Ford Algorithm (벨만-포드 알고리즘)

Bellman-Ford 알고리즘은 Dijkstra 알고리즘과 마찬가지로

단일 정점에서 각 정점까지의 최단거리를 구하는 알고리즘이다.

 

시작점은 1번 정점이다.

dist배열은 시작점으로부터의 거리를 나타내고 INF로 초기화 되어있다.

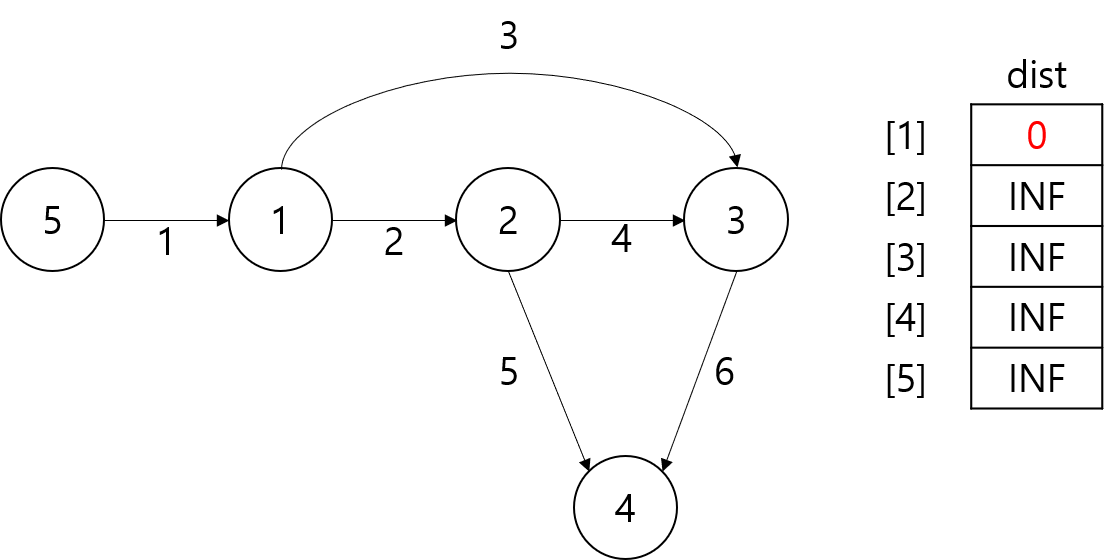
초기상태는 아래와 같으며 그래프의 구현은 인접 행렬(Adjacency Matrix) W로 되어있다.

 

시작점이 1번 정점이기 때문에 dist[1]을 0으로 갱신한다.

한 정점과 인접한 정점을 중심으로 갱신을 이어나간 Dijkstra 알고리즘과는 달리

Bellman-Ford 알고리즘은 매 수행마다 모든 간선(edge)에 대해 갱신을 진행한다.

한 간선이 정점 i에서 정점 j로 이어진다고 할 때, 다음 연산을 통해 갱신이 진행된다.

 

dist[j]=min(dist[j],dist[i]+W[i][j])

 

위 그래프는 총 6개의 간선으로 이루어져있다.

각 간선별로 살펴보자면,

1. (5->1)

dist[1]=min(dist[1],dist[5]+W[5][1])=min(0,INF+1)=0, 갱신 X

2. (1->2)

dist[2]=min(dist[2],dist[1]+W[1][2])=min(INF,0+2)=2, 갱신 O

3. (1->3)

dist[3]=min(dist[3],dist[1]+W[1][3])=min(INF,0+3)=3, 갱신 O

4. (2->3)

dist[3]=min(dist[3],dist[2]+W[2][3])=min(3,INF+4)=3, 갱신 X

5. (2->4)

dist[4]=min(dist[4],dist[2]+W[2][4])=min(INF,INF+5)=INF, 갱신 X

6. (3->4)

dist[4]=min(dist[4],dist[3]+W[3][4])=min(INF,INF+6)=INF, 갱신 X

로 2번의 갱신이 이루어졌다. 갱신된 dist배열은 다음과 같다.

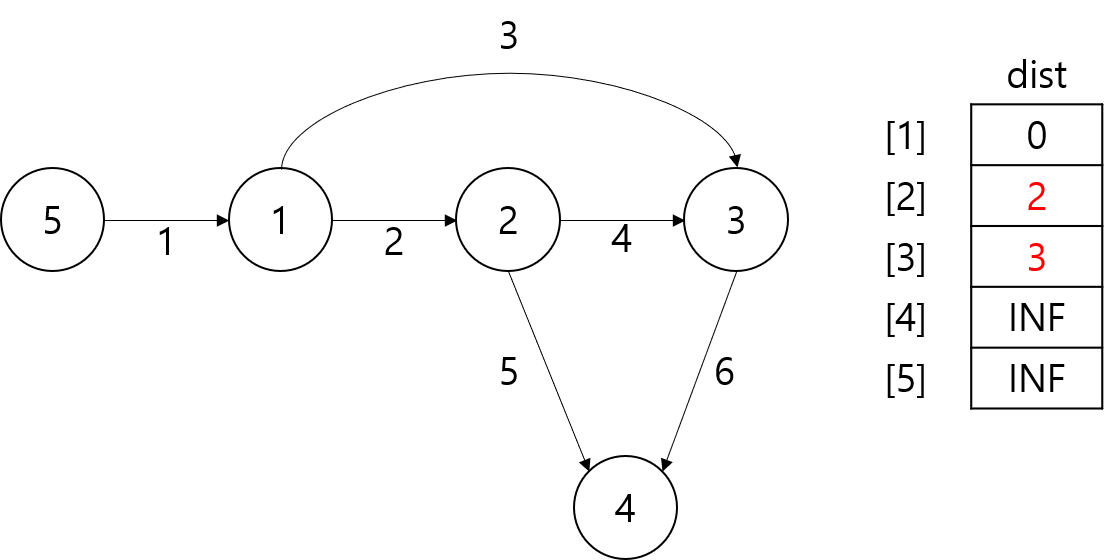
이번에도 모든 간선에 대해 갱신을 시도해보자.

1. (5->1)

dist[1]=min(dist[1],dist[5]+W[5][1])=min(0,INF+1)=0, 갱신 X

2. (1->2)

dist[2]=min(dist[2],dist[1]+W[1][2])=min(2,0+2)=2, 갱신 X

3. (1->3)

dist[3]=min(dist[3],dist[1]+W[1][3])=min(3,0+3)=3, 갱신 X

4. (2->3)

dist[3]=min(dist[3],dist[2]+W[2][3])=min(3,2+4)=3, 갱신 X

5. (2->4)

dist[4]=min(dist[4],dist[2]+W[2][4])=min(INF,2+5)=7, 갱신 O

6. (3->4)

dist[4]=min(dist[4],dist[3]+W[3][4])=min(7,3+6)=7, 갱신 X

로 오직 1번의 갱신만 일어났다.

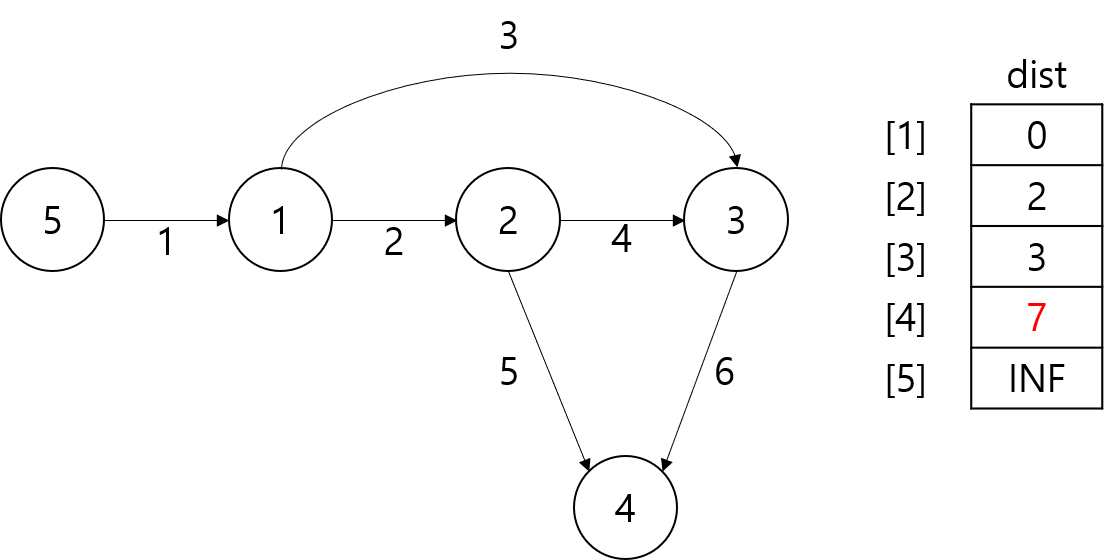
위 과정을 2번 더, 총 4번을 진행한 결과는 다음과 같다.

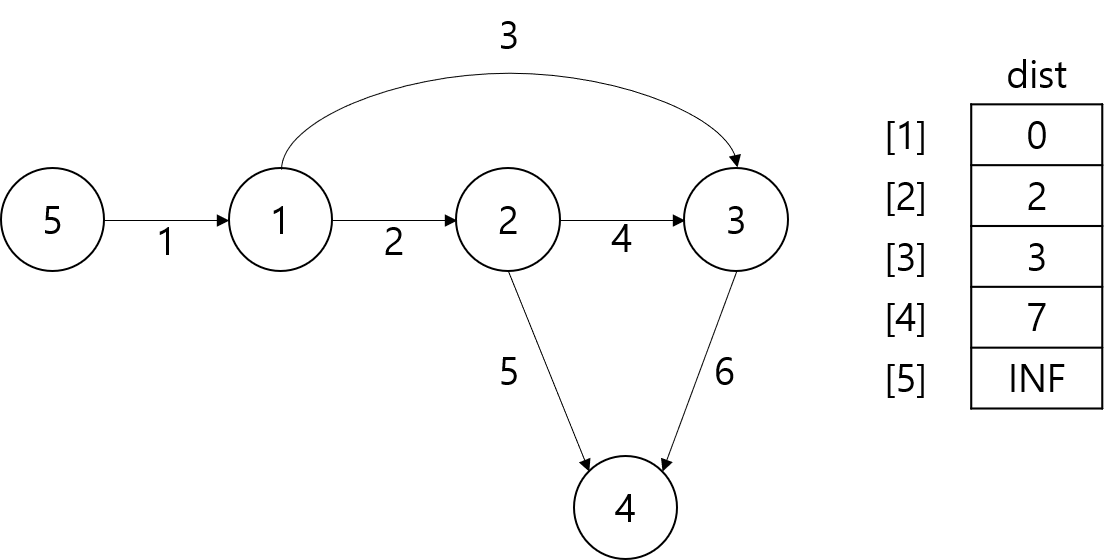
여기서 반복 횟수인 4가 의미하는 것은 (정점의 수)-1 이다.

해당 횟수는 위 그림처럼 모든 정점이 일렬로 놓여있는 경우에도

시작지점인 정점 1에서 모든 정점과의 거리를 계산할 수 있는 반복 횟수이다.

 

 

인접한 정점과의 거리만 갱신하는 Dijkstra 알고리즘과는 달리,

매번 모든 간선을 검토한다는 점에서 Bellman-Ford 알고리즘은 비효율적인것처럼 보인다.

 

그럼에도 이 알고리즘을 알고 있어야 하는 이유는 무엇일까?

바로 Bellman-Ford 알고리즘은 가중치(Weight)가 음수인 경우를 다룰 수 있기 때문이다.

 

Dijkstra 알고리즘의 경우,

dist[j]=min(dist[j],dist[i]+W[i][j])

의 식에서 갱신이 이뤄지면 Priority Queue에 삽입했다.

위 그래프에서 Dijkstra 알고리즘을 따라 정점 1에서부터의 거리를 계산하다 보면 어느순간

dist[1]=0, dist[2]=1, dist[3]=3로 dist 배열이 갱신될 것이고, 큐(우선순위 큐)에는 정점 3이 들어가있을 것이다.

문제는 정점 3에서 인접한 정점과의 거리를 계산할때 발생한다.

정점 3은 정점 2와 인접해있다.

게다가 dist[2]=1, dist[3]+W[3][2]=0이므로 dist[2]가 0으로 갱신되고 정점 2는 큐에 삽입된다.

 

다시, 정점 2는 정점 3과 인접해있고

dist[3]=3, dist[2]+W[2][3]=2이므로 dist[3]이 2로 갱신되고 정점 3은 큐에 다시 삽입된다.

이 과정이 계속해서 반복되며 무한루프에 빠지게 된다.

 

위의 그림처럼 사이클에서 모든 간선의 가중치의 합이 음인 사이클을 음의 사이클(Negative Cycle)이라고 하고,

Dijkstra 알고리즘은 음의 사이클이 있는 그래프에서 단일 정점으로부터의 최단거리를 구하는 문제에는 적합하지 않다.

 

하지만, Bellman-Ford 알고리즘에서는 (정점의 수)-1회 만큼의 과정을 통해

이미 dist 배열이 완성되었기 때문에 무한 루프에 빠지지 않는다.

 

오히려, (정점의 수)-1회만큼의 과정 이후, dist의 갱신이 한번이라도 이루어지면

해당 그래프가 음의 사이클(Negative Cycle)을 가지고 있다는 것을 알아채기도 한다.