[Algorithm] Floyd-Warshall Algorithm(플로이드-와샬 알고리즘)

Floyd-Warshall 알고리즘은 기존에 포스팅했던 Dijkstra 알고리즘이나 Bellman-Ford 알고리즘과 다르게,

모든 정점들 사이의 최단거리를 계산하는 알고리즘이다.

 

그래프의 초기 상태는 다음과 같다.

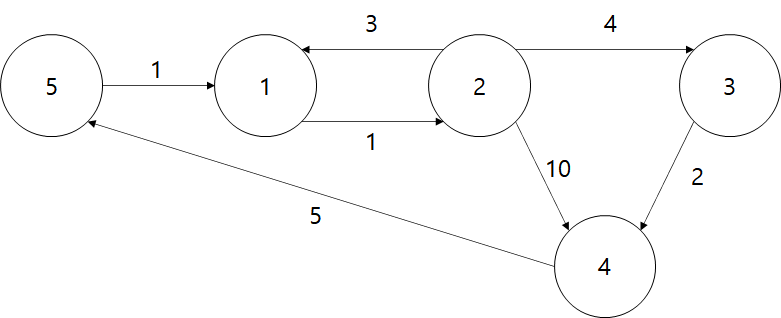
두 정점사이의 거리를 나타내는 dist 배열을 나타내보자.

dist[i][j]는 정점 i에서 정점 j까지의 거리이다.

dist 배열의 초기값은 i==j일때는 0으로, 정점 i와 정점 j가 연결되어있다면 두 정점을 잇는 간선의 가중치로,

두 정점이 연결되어있지 않다면 적당히 큰 수인 INF로 설정했다. 초기 dist배열의 모습은 아래와 같다.

초기 dist 배열

 

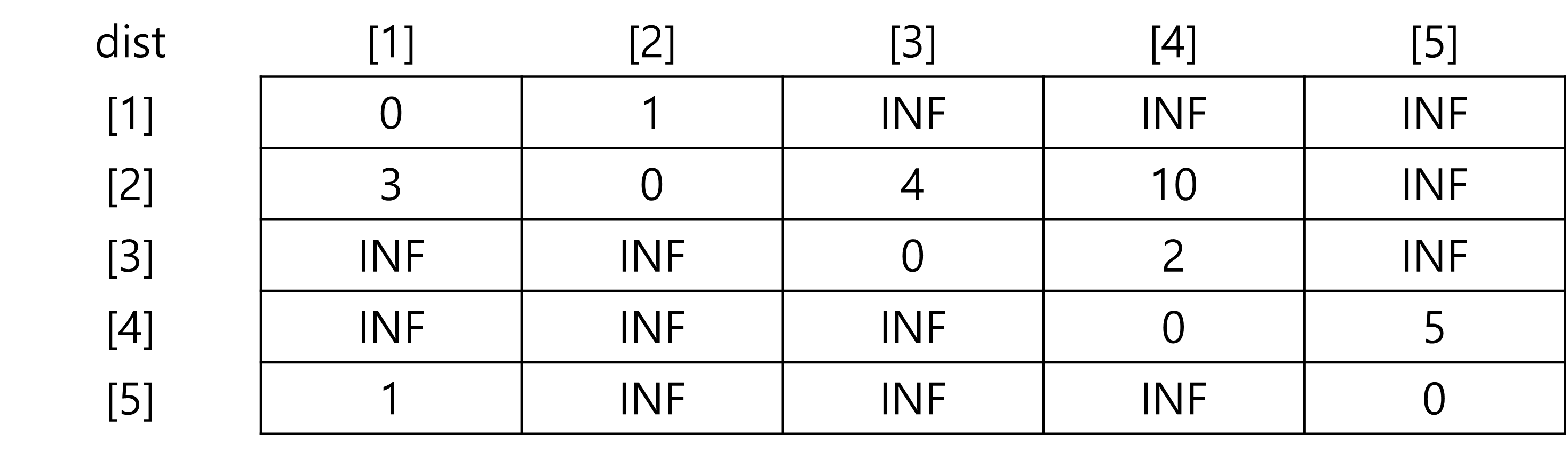
Floyd-Warshall 알고리즘의 핵심은 정점 k(1<=k<=5)에 대해 dist 배열의 모든 원소를 순회하며

dist[i][j]=min(dist[i][j],dist[i][k]+dist[k][j])를 진행하는 것이다.

 

위 코드가 의미하는 바는 정점 i에서 정점 j로 갈 때, 기존에 알고있던 길로 가는 것(dist[i][j])과 중간 지점(k)을 거친 것(dist[i][k]+dist[k][j]) 중 최소값으로 dist[i][j]를 업데이트하는 것이다.

 

의사 코드로 표현하자면 다음과 같다.

for(int k=1;k<=N;k++){
	for(int i=1;i<=N;i++){
		for(int j=1;i<=N;j++){
			dist[i][j]=min(dist[i][j],dist[i][k]+dist[k][j]);
		}
	}
}

이 방식으로 업데이트를 진행해보겠다.

단 i==j인 경우는 dist를 0으로 초기화했기 때문에 양의 가중치를 갖는 그래프에서는 항상 최소값이 되기 때문에 생략한다. 총 비교횟수가 많아(5^3) 업데이트가 발생하는 경우만 서술하도록 하겠다.

1. k=1

(1) (5->2)

dist[5][2]=min(dist[5][2],dist[5][1]+dist[1][2])=min(INF,1+1)=2

정점 1을 경유지로 했을 때, 업데이트 된 dist 배열

2. k=2

(1) (1->3)

dist[1][3]=min(dist[1][3],dist[1][2]+dist[2][3])=min(INF,1+4)=5

(2) (1->4)

dist[1][4]=min(dist[1][4],dist[1][2]+dist[2][4])=min(INF,1+10)=11

(3) (5->3)

dist[5][3]=min(dist[5][3],dist[5][2]+dist[2][3])=min(INF,2+4)=6

(4) (5->4)

dist[5][4]=min(dist[5][4],dist[5][2]+dist[2][4])=min(INF,2+10)=12

정점 2를 경유지로 했을 때, 업데이트 된 dist 배열

3. k=3

(1) (1->4)

dist[1][4]=min(dist[1][4],dist[1][3]+dist[3][4])=min(11,5+2)=7

(2) (2->4)

dist[2][4]=min(dist[2][4],dist[2][3]+dist[3][4])=min(10,4+2)=6

(3) (5->4)

dist[5][4]=min(dist[5][4],dist[5][3]+dist[3][4])=min(12,6+2)=8

정점 3을 경유지로 했을 때, 업데이트 된 dist 배열

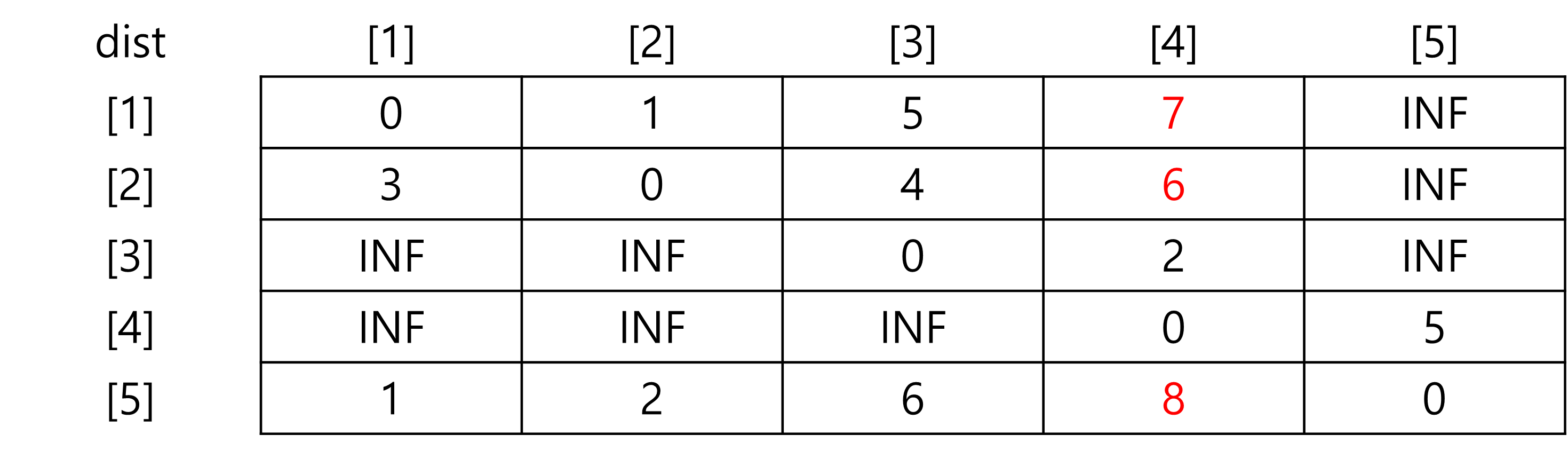
4. k=4

(1) (1->5)

dist[1][5]=min(dist[1][5],dist[1][4]+dist[4][5])=min(INF,7+5)=12

(2) (2->5)

dist[2][5]=min(dist[2][5],dist[2][4]+dist[4][5])=min(INF,6+5)=11

(3) (3->5)

dist[3][5]=min(dist[3][5],dist[3][4]+dist[4][5])=min(INF,2+5)=7

정점 4를 경유지로 했을 때, 업데이트 된 dist 배열

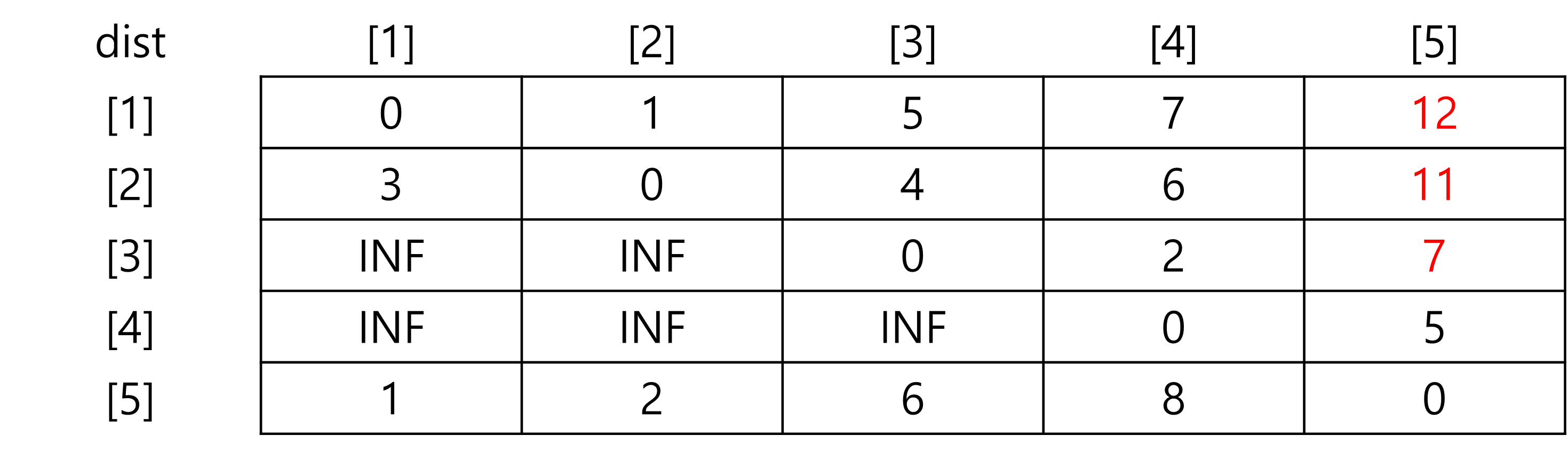
5. k=5

(1) (3->1)

dist[3][1]=min(dist[3][1],dist[3][5]+dist[5][1])=min(INF,7+1)=8

(2) (3->2)

dist[3][2]=min(dist[3][2],dist[3][5]+dist[5][2])=min(INF,7+2)=9

(3) (4->1)

dist[4][1]=min(dist[4][1],dist[4][5]+dist[5][1])=min(INF,5+1)=6

(4) (4->2)

dist[4][2]=min(dist[4][2],dist[4][5]+dist[5][2])=min(INF,5+2)=7

(5) (4->3)

dist[4][3]=min(dist[4][3],dist[4][5]+dist[5][3])=min(INF,5+6)=11

정점 5를 경유지로 했을 때, 업데이트 된 dist 배열

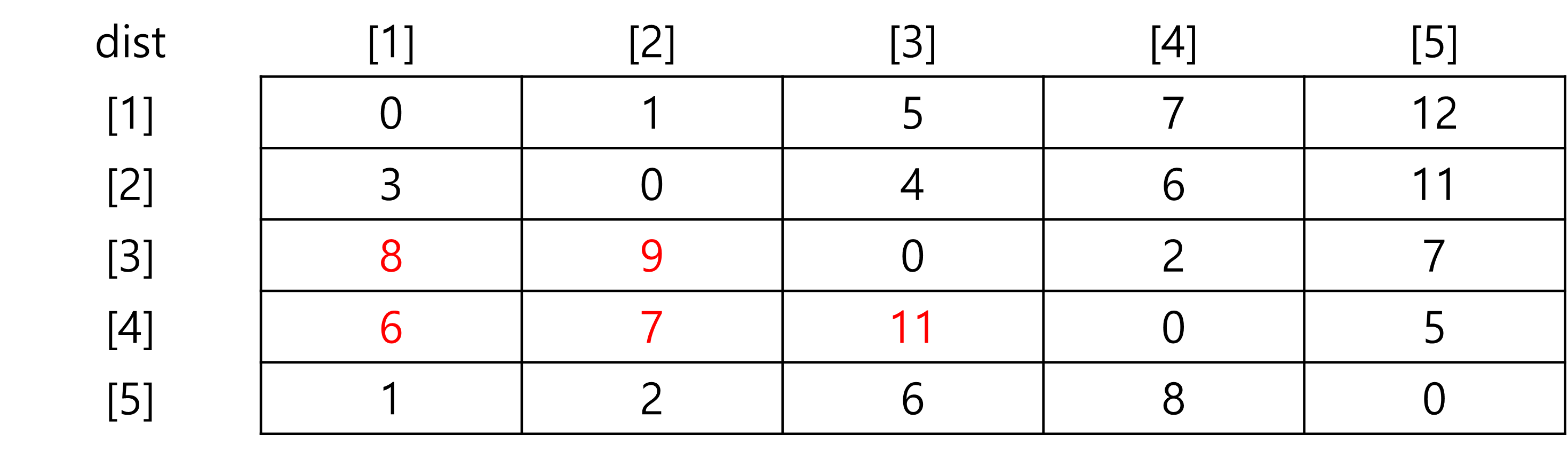
모든 과정이 완료된 dist 배열은 아래와 같다.

최종 dist 배열

※ 생각해 볼만한 점

위 그래프를 가지고 전체 과정을 한번더 진행해 봐도 dist의 업데이트는 일어나지 않는다.

dist의 한 원소 A를 업데이트 하는 과정에서 dist의 원소 B를 사용하는 데,

B가 갱신되면, B를 가지고 업데이트 했던 A의 값도 같이 변경되어야 하는 것이 아닌가...?

각 경유지 k에 대해 한번씩 dist 배열을 순회한것만으로 최적의 해라고 어떻게 보장할 수 있을까...?