이번 포스팅에서는 LeNet-5라고 알려져 있는 Yann LeCun이 1998년에 발표한 "Gradient-Based Learning Applied to Document Recognition"을 읽고 정리해 보도록 하겠습니다.
I. Introduction
본 논문에서 시사하고자 하는 바는 사람이 일일이 설계한 특징(?)들에 의존하기보단, 자동화된 학습(automatic learning)에 의존하는 것이 패턴인식에 더 효과적이라는 것입니다.
Introduction에서는 두 가지 케이스를 제시했습니다. 첫 번째는 character recognition이고, 두 번째는 document understanding입니다.
character recognition의 경우 독립된 하나의 글자를 인식하는 문제입니다. 이러한 문제는 픽셀 이미지에 직접 동작하는 머신을 사용하는 것이 효과적이라고 하는데 우리가 알고 있는 CNN을 의미합니다. document understanding은 여러 개의 글자가 모인 문장, 여러 문장이 모인 문서를 이해하는 과정입니다. 이런 문제는 통합되고(unified) 신조가 뚜렷한(?)(well-principled) 디자인 패러다임을 사용하는 것이 효과적인데, Graph Transformer Networks가 바로 그것입니다.
기존의 패턴 인식 체계는 아래 아래 그림과 같이 automatic learning technique과 hand-crafted algorithm의 조합으로 구성되었습니다.

첫번째 모듈에 해당하는 feature extractor는 입력 패턴을 저 차원의 백터나 짧은 문자열로 변환합니다. 이러한 변환된 형태는 쉽게 매칭 되거나 비교되고, 입력의 class가 바뀌지 않는 선에서의 변형에 강인합니다. 이러한 feature extractor는 사전 지식이 어느 정도 필요하며 과업(task) 별로 특정됩니다. 보통 수작업으로 설계되기 때문에 가장 시간을 많이 투자하는 부분 중 하나입니다. 반면에 두 번째 모듈에 해당하는 classifier는 feature extractor에 비해 보편적이고 학습 가능합니다.
이러한 구조에서 발생할 수 있는 문제점은 인식의 성능이 feature extractor를 설계하는 사람에 의해 좌우되고, 매번 다른 문제에 새로운 feature extractor를 설계해야 하기 때문에 daunting한 과정입니다.
왜 매번 이런 고생을 해야하는 feature extractor을 굳이 사용해야만 했던 걸까요? 그 이유는 당시 classifier가 저 차원의 공간에만 국한되어있었기 때문입니다. 그러나 다음 3가지 요인에 의해 판도가 바뀌게 됩니다.
첫번째로 컴퓨터 성능의 향상으로 알고리즘을 개선시키는 것이 아닌 무작정(brute-force) 계산하는 방법이 가능해지게 됐습니다. 두 번째로 데이터의 크기가 증가하여 설계자들이 hand-crafted feature extraction보다는 real data에 의존하게 됐습니다. 세 번째는 매우 중요한 요인인데 고차원의 입력을 다룰 수 있고 복잡한 결정을 내릴 수 있는 머신러닝 기술이 등장한 것입니다. 바로 뒤에 언급된 backpropagation으로 학습된 multi-layered neural networks가 그 예입니다.
본 논문의 Section I, II에서는 handwritten character recognition을 다룰 예정이고 Section III에서 다른 learning technique들과 비교합니다. Section IV 이후로는 document recognition을 다루고 Graph Transformer Network를 소개하지만 본 포스팅에서 다루지는 않을 예정입니다.
A. Learning from Data
(논문 작성일 기준) 최근 신경망 분야에서 대중화된 방법은 gradient-based learning이라고 합니다.
learning machine은 다음 함수를 계산합니다.

여기서 Z^p는 p번째 입력 패턴이고, W는 adjustable(trainable)한 매개변수입니다. 함수의 출력 Y^p는 패턴 Z^p에 대해 예측한 class의 label이거나 각각의 class에 관련된 확률 또는 점수입니다.
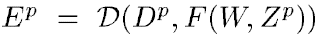
위 loss function은 p번째 패턴의 실제 label을 의미하는 D^p와 machine의 출력 사이의 불일치(discrepancy)를 측정합니다. 다음 avarage loss function은 {(Z^1, D^1),..., (Z^p, D^p)}까지의 평균 오차를 의미합니다.

학습 과정에서 해야할 것은 E_train(W)를 가장 작게 만드는 W값을 찾는 것입니다. 하지만 실제로 중요한 것은 train data가 아닌 test data에 대해서 오차를 줄여야 하는 것입니다. 다른 연구에 따르면 예상되는 E_test과 E_train의 관계는 다음 식에 근접한다고 합니다.
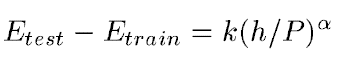
여기서 P는 train data의 크기를 의미합니다. h는 machine의 복잡도를 의미합니다. α는 0.5와 1.0 사이의 수이고 k는 상수입니다. 즉, train data의 크기가 커지고 machine이 단순해진다면 train data에서의 오차와 test data에서의 오차의 차이가 줄어든다는 것입니다. 게다가 h(machine의 복잡도)가 증가하면 E_train은 감소합니다. 그렇기 때문에 h가 증가하면 E_train은 감소하고 E_test와 E_train 사이의 차이는 증가하게 됩니다. 대부분의 학습 알고리즘은 E_test와 E_train의 차이를 보면서 E_train을 최소화시키는 방법을 시도합니다. 이를 structural risk minimization이라고 합니다. 실제로는 다음을 최소화하는 방향으로 학습합니다.
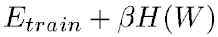
여기서 H(W)는 regularization function이고 β는 상수입니다. H(W)는 매개변수 공간에서 고용량의 부분집합을 취하도록 선택됩니다. 그렇기 때문에 H(W)를 최소화하는 것은 매개변수 공간의 접근 가능한 부분집한이 제한되는 것이므로 E_train을 최소화하는 것과 E_test와 E_train 간의 차이를 최소화하는 것 사이의 trade-off를 제한하는 것입니다.
B. Gradient-Based Learning
loss function은 loss function에서 매개 변수 값의 작은 변화의 영향을 측정하는 것으로 쉽게 최소화가 됩니다. 이런 측정은 loss function의 현재 매개변수에서의 gradient를 이용합니다. 효율적인 학습 알고리즘은 gradient vector가 수적(numerically)이 아닌 분석적으로(analytically)구해질 때 고안될 수 있다고 합니다. 수적은 무엇이고 분석적은 무엇일까요? 두 차이를 다음과 같이 설명하기도 합니다.

제가 이해한 바로는 분석적이라는 것은 수학적으로 이미 명확하게 계산을 끝냈다는 것을 의미하는 것 같습니다. 분석적으로 gradient vector를 구해야 하는 것은 수많은 연속적인 매개변수 값에 대한 gradient-based 학습 알고리즘의 기반이 됩니다. gradient-based learning 중 gradient descent 알고리즘이 하고자 하는 것은 다음과 같습니다.
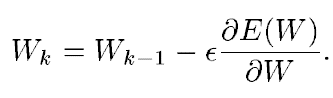
W는 실수의 매개변수 집합입니다. loss function E(W)는 연속적이고 미분 가능합니다. ε는 스칼라 상수입니다.
보다 정교한 과정을 위해서 ε를 변수로 두거나, 대각 행렬로 두거나 Hessian 행렬의 역행렬을 사용할 수도 있습니다.
대중적인 최적화 과정은 online update라고 불리기도 하는 stochastic gradient 알고리즘입니다. stochastic gradient 알고리즘은 매개변수를 noisy하거나 approximated 된 average gradient를 사용하여 갱신합니다.
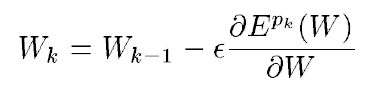
stochastic gradient 방법은 보통의 gradient descent 방법보다 변동이 심하지만 보통 더 빠르게 수렴합니다.
C. Gradient Back-Propagation
gradient-based learning 과정은 1950년대부터 소개되었지만 linear system에 한정되어 사용되었습니다. 그러나 다음 3가지 사건으로 인해 복잡한 머신러닝 과정에서도 gradient-based learning이 유용하다고 밝혀지게 됩니다.
첫번째로 loss function의 local minima 문제가 실제로는 큰 문제가 아니라는 것입니다. Boltzman machine과 같은 non-linear gradient-based learning technique이 성공함에 따라 local minima가 주요한 장애물이 아니라는 것이 밝혀졌습니다.
두번째로 Rumelhart, Hinton, Williams에 의해 back-propagation 알고리즘이 non-linear system에서 대중화된 것입니다. 세 번째는 back-propagation 과정이 sigmoidal unit을 사용한 multi-layer neural network에 적용되면 복잡한 머신러닝 과업을 해결할 수 있다는 것이 밝혀졌습니다.
back-propagation의 기본 아이디어는 출력에서 입력으로 가면서 gradient가 효율적으로 계산된다는 것입니다. back-propagation의 간단한 도출은 Section I-E.에서 언급된다고 합니다.
D. Learning in Real Handwriting Recognition Systems
논문 작성 당시 손글씨 인식에서 가장 성공적인 결과를 낸 것은 neural network입니다. Section III에서 다른 방법들과 비교를 하겠지만 gradient-based learning 방법이 다른 모든 방법보다 좋았고 Convolutional Network라는 신경망이 pixel image에서부터 바로 feature를 추출했습니다.
손글씨 인식에서 가장 어려운 부분중 하나는 segmentation이라고 불리는 단어나 문장에서 각각의 글자를 분리하는 것입니다. 논문 작성 당시 표준이라고 불리는 방법은 Heuristic Over-Segmentation이었습니다. 이는 heuristic 한 이미지 처리 기술을 이용하여 가능성 있는 많은 경우의 글자 간 분리를 진행합니다. 그리고 recognizer에 의해 후보들 중 가장 높은 점수를 낸 조합을 채택합니다. 이러한 모델의 경우 heuristic 하게 자른 이미지의 품질과 recognizer가 여러 후보들 중 적절하게 분리된 글자를 얼마나 잘 식별하는가에 따라서 성능이 갈리게 됩니다. 하지만 이는 부적절하게 분류됐다는 label을 갖는 데이터가 없기 때문에 recognizer를 학습시키기 어렵게 됩니다. 가장 간단한 해결책은 segmenter를 거친 이미지에 일일이 labeling 하는 것인데 매우 비용이 많이 들고 어려운 작업입니다. 이에 본 논문의 Section V, VII에서는 GTN을 이용한 방법을 사용하긴 하는데 본 포스팅에서 다루지는 않을 예정입니다.
E. Globally Trainable Systems
실제 패턴 인식 시스템은 이전에 언급한 바와 같이 여러 모듈로 구성되어 있습니다. 대개 recognizer를 따로 학습시킨 다음 전체 모듈을 모아 성능을 향상시키는 방식으로 매개변수를 조정하는데 이는 비용이 매우 많이 드는 작업입니다. global error를 최소화시키는 방향으로 시스템 전체를 학습시키게 된다면 보다 나은 방안이 될 수 있습니다.
gradient-based learning을 사용하게 되면 미분 가능한 loss function E, 학습 가능한(tunable) 매개변수 W에 대해 E의 local minimum을 계산할 수 있게 됩니다. 하지만 시스템(모델)이 복잡해 진다면 gradient-based learning을 적용시키기 어려워 보입니다.
시스템 전체의 loss function E^p가 미분가능함을 보장하기 위해 미분 가능한 모듈들의 feed-forward network로 전반적인 시스템을 구성했습니다. 여기서 feed-forward란 순방향이라는 뜻으로 노드 간의 연결이 순환을 형성하지 않는다는 것입니다. 다시 논문으로 돌아와서 각각의 모듈에 의해 구현된 함수들은 연속이고 대부분의 경우에서 미분 가능해야 합니다. 위를 만족할 경우, back-propagation 절차의 일반화를 사용하여 시스템 내의 모든 매개변수에 대해 gradient를 효율적으로 계산할 수 있게 됩니다.
시스템이 다음 함수를 구현하는 모듈들로 구성되어있다고 가정해봅니다.

X_n은 모듈의 출력을 의미하는 벡터이고, W_n은 학습 가능한 모듈의 매개변수입니다. X_(n-1)은 이전 모듈의 출력입니다. X_0는 모델의 첫 입력이며 입력 패턴인 Z^p와 같습니다. 시스템 전체의 loss function E^p를 각각 W_n, X_(n-1)에 대해 편미분 한 것은 다음과 같습니다.
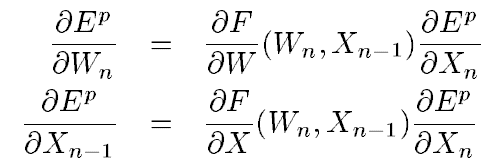
첫 번째 수식은 E^p(W)의 일부 항의 gradient를 계산합니다. 두 번째 수식은 back-propagation 과정입니다. 위 수식은 편도 함수의 벡터로 구성된 야코 비안(Jacobian)의 곱을 사용하는데, 보통 야코 비안을 미리 계산하지 않고 그냥 곱을 구하는 게 쉽습니다.
II. Convoultional Neural Networks for Isolated Charater Recognition
전통적인 패턴 인식 시스템은 hand-designed feature extractor와 trainable classifier로 구성됩니다. Trainable classifier를 fully-connected multi-layer network로 사용 가능합니다. feature extractor로 fully-connected multi-layer network를 사용하는 것이 효과적이긴 했으나 다음과 같은 문제점이 발생했습니다.
우선, 보통의 이미지는 크기가 크기 때문에 많은 매개변수들이 필요로 하고, 많은 매개변수를 학습시키기 위해 더 많은 데이터를 요구하게 됩니다. 또한 메모리를 많이 잡아먹습니다. 가장 큰 결점은 입력 데이터에 약간의 왜곡만 취해져도 아주 다른 데이터라고 인식하는 것입니다.
다음으로, fully-connect network는 입력의 topology를 무시합니다. 이미지의 경우 인접한 픽셀이 상당히 깊은 연관성을 갖고 있습니다. 후술 할 Convolutional Neural Network는 이러한 문제점을 해결해줍니다.
A. Convolutional Networks
Convoultional Neural Network는 약간의 shift, scale, distortion invariance에도 견디기 위해 local receptive fields, shared weights, sub-sampling의 3가지 아이디어를 조합했습니다. 아래 사진은 LeNet-5의 구조입니다.
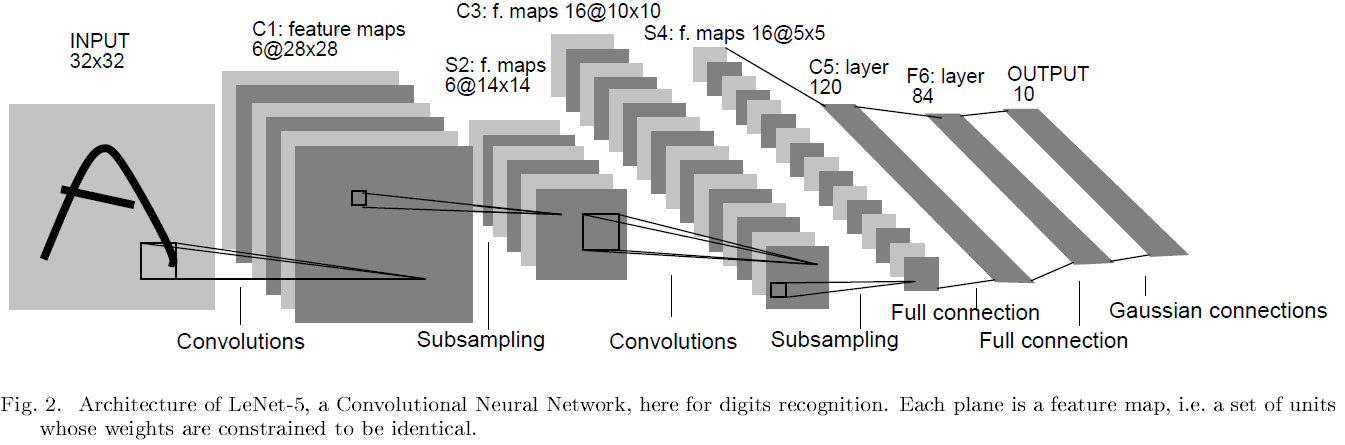
input plane은 size-normalized 하고 centered 된 이미지를 입력으로 받습니다. layer의 각각의 unit은 이전 layer의 근처에 위치한 unit들에서 입력을 받아옵니다(local receptive fields). local receptive fields를 사용하게 되면 edges, end-points, corners와 같은 저차원의 visual feature를 추출할 수 있게 됩니다. 이러한 feature들을 하위의 layer들에서 조합하여 고차원의 visual feature를 감지할 수 있게 됩니다. 또한, local receptive fields에서 추출한 저차원의 feature들은 이미지 전체로도 유의미한 feature이기 때문에 이미지에 약간의 왜곡이 주어지더라도 같은 weight vector를 갖게 됩니다.
layer의 unit들은 같은 weight를 공유하는 plane에 의해 조직됩니다. 이러한 plane의 출력들은 feature map이라고 불립니다. feature map의 unit들은 이미지의 다른 부분에서도 같은 연산을 하도록 제한됩니다. 완전한 convoultional neural network는 각각의 위치에서 여러 개의 feature를 추출하기 위해 weight vector가 다른 여러개의 feature map으로 구성되어 있습니다. 위 사진의 첫 번째 layer C1이 그 예시입니다. C1은 6개의 feature map을 구성합니다. feature map의 unit은 5x5의 receptive field라고 하는 입력을 갖고 있습니다. 그래서 25개의 trainable coefficient에 1개의 trainable bias가 됩니다. feature map의 인접한 unit의 receptive field는 이전 layer의 인접 unit들의 중심에 위치하여 겹치게 됩니다. 각각의 feature map은 서로 다른 weight를 가지며, 서로 다른 local feature을 추출합니다. feature map의 작동은 convolution으로 이뤄집니다. 그래서 이런 LeNet-5와 같은 network를 convolutional network라고 칭합니다. 이러한 network의 장점은 입력 이미지에 shift를 줘도 feature map 출력이 똑같이 shift 되어 결국 기존과 출력 값이 같게 됩니다. 이러한 속성이 입력 image의 shift나 distortion에 강하게 해 줍니다.
한번 feature가 감지되면, 해당 feature의 정확한 위치보다는 다른 feature에 대한 상대적인 위치가 더욱 중요하게 됩니다. 논문에서는 숫자 7을 예시로 들었습니다. 좌측 상단엔 수평의 에지가, 우측 상단엔 코너가, 아랫부분은 수직의 엣지가 있다면 해당 이미지가 7이라고 할 수 있습니다. 이러한 특징의 정확한 위치는 패턴 식별과 무관할 뿐만 아니라 글자들 각각에 따라 다를 수 있으므로 해로울 수 있습니다. 이렇게 정확도를 줄이는 방법으로 feature map의 부분적인 해상도를 줄이는 방법이 있습니다. 이를 담당하는 layer를 본 논문에서는 sub-sampling layer라고 칭하지만 저에게는 pooling이 더 익숙합니다. LeNet-5의 두 번째 layer는 sub-sampling layer입니다. 각각의 receptive field는 2x2의 unit을 가집니다. 이런 unit은 2x2(=4)의 평균을 계산하고 해당 unit의 trainable coefficient와 곱한 다음 trainable bias와 더합니다. 그리고 sigmoid function을 적용시킵니다. 이전 convolutional layer와는 다르게 인접한 unit들 간의 overlapping은 하지 않습니다. 따라서 unit이 2x2이기 때문에 행의 수와 열의 수가 이전 layer에 비해 반으로 줄어들게 됩니다. 여기서 sigmoid function은 작은 weight에 대해서는 준선형(quasi-linear) 모드로 unit이 연산하고, sub-sampling layer가 입력을 blur 하는 동작을 수행합니다. 큰 weight에 대해서는 sub-sampling unit이 bias에 따라 "noisy OR" 또는 "noisy AND"의 기능을 하는것처럼보입니다. 이후 layer들은 bi-pyramid의 형태를 띠게 되는데, sub-sampling layer에서 줄어든 만큼 convolutional layer에서 feature map의 수가 늘어나는 것을 반복하는 형태입니다.
모든 weight들은 back-propagation을 통해 학습되기 때문에 convolutional network는 앞서 언급한 pattern recognition system의 feature extractor가 아예 합쳐진 것 처럼 보입니다. 그리고 weight sharing technique이 machine의 capacity를 줄여 Section I-A에서 언급한 test error와 train error 사이의 격차를 줄일 수 있을 것이라고 생각됩니다. 위 그림은 340,908의 connection이 있지만 weight의 수는 고작 60,000개에 불과합니다.
B. LeNet-5
LeNet-5는 7개의 layer로 구성되어있습니다. 입력으로 32x32의 이미지를 사용합니다. 이는 데이터베이스의 가장 큰 글자보다 더 큰데, stroke end-point나 corner와 같은 뚜렷한 feature들은 첫 번째 convolutional layer의 중간 receptive field에서 나타나기 때문입니다. 배경은 -0.1, 글자에 해당하는 검은색 부분은 1.175로 인식시키기 위해 입력 이미지에 normalize를 진행했습니다.
C1 layer는 6개의 feature map을 갖고 있습니다. feature map은 입력의 5x5 씩 연결되어있습니다.
S2 layer는 sub-sampling layer로, C1의 feature map에서 2x2 씩 받아옵니다.
C3 layer는 16개의 feature map을 갖고 있습니다. 또한 S2를 지난 feature map의 5x5 씩 연결되어있습니다. 아래 테이블은 S2의 어떤 feature map이 C3의 어떤 feature map과 연결되어 있는지 보여줍니다.
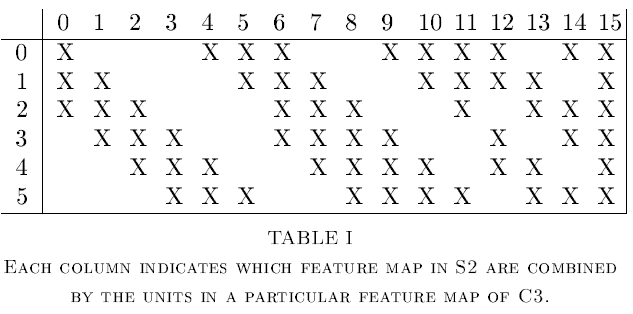
S2의 모든 feature map이 C3의 모든 feature map과 연결되지 않은 이유는 두 가지가 있습니다. 첫 번째로, 불완전한 연결 체계는 연결의 수를 합리적인 범위 내에서 유지합니다. 더 중요한 것은, network의 대칭을 파괴합니다. 다른 feature map은 다른 feature를 추출합니다.
S4 layer는 5x5의 16개의 feature map으로 구성되어있습니다. C3 layer의 feature map에서 2x2 씩 받아옵니다.
C5 layer는 120개의 feature map을 가집니다. 5x5 씩 S4 layer에서 받아오나, S4의 feature map이 5x5 이기 때문에 C5의 feature map은 1x1입니다.
F6 layer는 84개의 unit이 있습니다. C5와 fully-connected 되어 있습니다.
마지막의 output layer는 Euclidean Radial Basis Function(RBF)으로 구성되어 있습니다. 아래 식을 이용해 각각의 RBF의 출력(y_i)을 구할 수 있게 됩니다.

특정 RBF는 입력 패턴과 정답 패턴 간의 차이를 측정하는 벌점 항(penalty term)으로 해석될 수 있습니다. 확률론적으로는 가우시안 분포의 unnormalized negative log-likelihood로 해석될 수 있습니다. RBF는 F6 layer에서 target vector 역할을 합니다. F6 layer의 weight들은 +1 아니면 -1인데 이는 sigmoid의 최대 곡률과 일치합니다. 그렇기 때문에 loss function의 느린 수렴을 야기하는 시그모이드 포화를 방지합니다.
C. Loss Function
LeNet-5에 사용하기 좋은 가장 간단한 loss function은 MSE에 해당하는 Maximum Likelihood Estimation(MLE)입니다. 식은 아래와 같습니다.
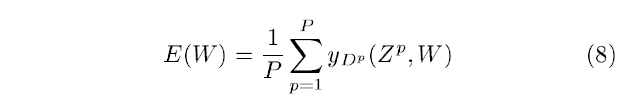
y_(D_p)는 D_p번째 RBF 유닛의 출력입니다. 대부분의 경우에 잘 맞은 loss function이지만, 세 가지의 결점이 있습니다.
첫 번째로, RBF의 매개변수들을 학습시키면 E(W)가 매우 작아지나, RBF의 모든 매개변수 벡터는 동일하기 때문에 결국 network의 입력은 무시한 채 모든 RBF의 출력이 0이 되게 됩니다. 이런 경우는 RBF의 매개변수를 학습시키지 않는다면 발생하지 않습니다.
두 번째론, class간의 경쟁이 없다는 것입니다. Maximum a Posteriori(MAP)를 사용하면 경쟁을 시킬수는 있습니다. MAP는 정답 class에 대한 posteriori probability를 최대화 시킵니다. 페널티의 관점에서는 MSE처럼 틀린 정답엔 큰 출력을, 올바른 정답엔 낮은 출력을 합니다.

두번째 항의 음이 경쟁을 담당합니다. 첫째항보다는 작거나 같아야 합니다. 상수 j는 양수이며 이미 매우 큰 클래스의 페널티가 더 이상 추가되는 것을 방지합니다.
그 전까지는 몇몇 모델들의 구조나 어떻게 생겼는 지 보기위해 논문들을 훑고만 말았는데, 본격적으로 읽고
이해한 선에서 정리를 시작해 보고자 CNN의 초기 버전(?)이라고 생각되는 해당 논문을 선택해보았습니다.
2021년기준으로는 상당히 오래된 논문이라 당시 background를 이해하기 상당히 어려웠습니다. 사실 LeNet-5만 있는 논문인줄 알았는데 알고 보니 46페이지 상당의 아주 긴 논문이었습니다. 읽다 지쳐 Section III. 실험 관련 부분은 정리하지 못했지만 나중에 시간되면 추가해 보도록 노력해 보겠습니다ㅜㅜ.
본 논문의 구현은 GitHub에서 확인하실 수 있습니다.
References
[1] http://yann.lecun.com/exdb/publis/pdf/lecun-01a.pdf
[2] https://arclab.tistory.com/150
[3] http://www.navisphere.net/1831/gradient-based-learning-applied-to-document-recognition/



댓글